本项目来源于国家自然科学基金重大项目课题2“高品质伺服电机磁场调制拓扑演变规律(51991382)”
起止时间2020年1月1日——2024年12月31日。
本项目工作概括如下:
一、主要研究内容
高转矩密度是各领域电机的共性追求,如何提升转矩密度一直是电机学科研究的主线与热点之一。近年来,研究人员研发出一类电枢与励磁磁场极数不等的永磁电机,该类永磁电机的定子齿槽除起到导磁功能外,还起到磁场调制的功能。在磁场调制作用下,低速多极励磁磁动势在定子上形成少极、高速的励磁磁场这种特殊的电磁现象使得这类永磁电机在外特性相当于“高速永磁电机+磁齿轮箱”,可以在相同电磁负荷条件下实现高转矩密度,这些优势使得磁场调制电机在航空航天、新能源发电、伺服加工、重型工业生产等众多领域拥有广阔工程应用前景。学术界将基于这种特殊工作原理的一类电机,包括游标永磁电机、磁通切换永磁电机、开关磁链永磁电机等统称为磁场调制永磁电机。为进一步实现伺服电机转矩密度提升,本课题对现有电机拓扑结构进行了分类总结,对现有伺服电机拓扑结构进行统一化,推导伺服电机拓扑结构的演变规律;基于此,提出多款新型高品质伺服电机拓扑结构,通过与常规伺服电机拓扑进行对比,总结得到适应于高端装备需求的高品质拓扑特征;以输出转矩最大化为目标,首次提出游标永磁电机气隙拓扑定向设计方法。本课题围绕“高品质伺服电机磁场调制拓扑演变规律”研究,重点介绍以下三部分研究成果:
(1)高品质伺服电机磁场调制拓扑演变规律;
(2)高性能磁场调制电机拓扑研究;
(3)建立电机稳态伺服品质与电机拓扑间的映射关系;
二、研究工作
2.1 高品质伺服电机磁场调制拓扑演变规律
提出磁场调制电机拓扑统一方法,解决了无理论支撑磁场调制永磁拓扑间技术进展借鉴的问题,为游标永磁电机的成果拓展至磁通切换、磁通反向永磁电机等其他磁场调制电机提供理论支撑与技术方案,并得到多工作磁动势谐波磁通反向、磁通切换永磁电机、极靴单连接磁通切换永磁电机等新型拓扑。
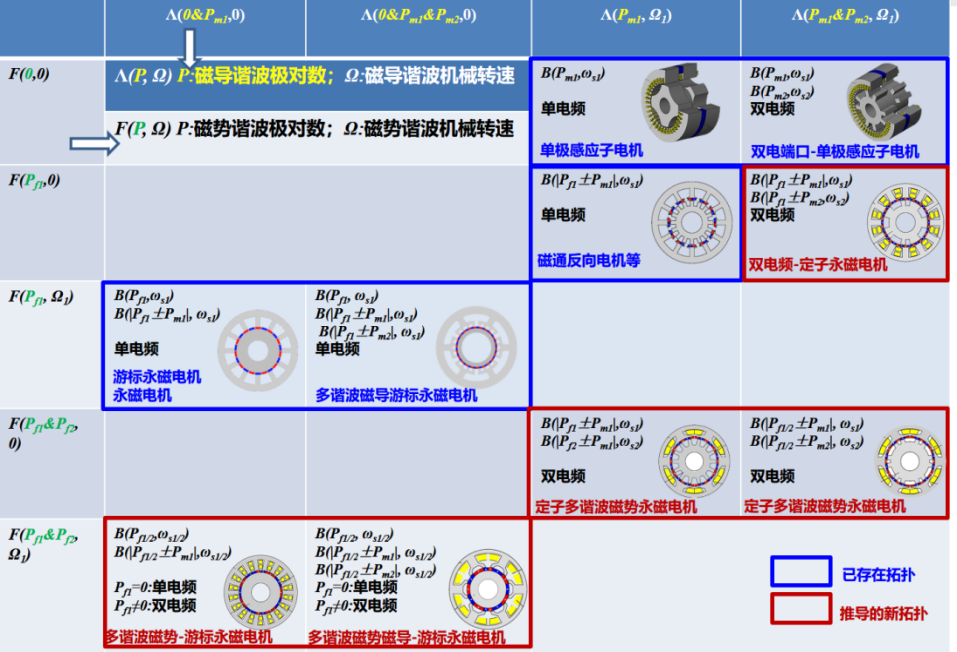
通过将电机视作三个功能单元—励磁单元、调制单元、电枢单元的集成,结合磁场调制单元理论分析,本课题将现有的多种高转矩密度电机热点拓扑,如游标永磁电机,开关磁链电机,磁通反相电机、横向磁通电机和双机电端口等电机的工作原理进行了统一,并建立磁场调制电机拓扑演变理论。以单运动自由度的电机为例,当励磁磁势工作谐波和调制磁导工作谐波分别最多有两个时,理论上可行的电机拓扑均归纳在图2-1中。
|
(a) |

|
(b) |
图2‑1磁场调制电机拓扑演变理论
例如,当电机磁动势函数为单谐波旋转形式,磁导具有常数项与静止的单谐波,就构成了游标永磁电机,如果其中静止磁导具有两个谐波分量,就进一步构成多谐波磁导游标永磁电机。通过这种数学上抽象的研究,揭示了该类电机的工作原理和构造方法,不仅可以将现有永磁电机,包括磁场调制电机都可以归类其中,更大大拓展了新型高性能电机电磁结构方案的研究思路。我们发现磁场调制电机拓扑体系中存在大量空白有待填补,这也是我们需要完成的重要工作之一。到目前为止,我们已经在空白区域发现了一些新的电机拓扑。接下来,将进一步对目前主要的磁场调制拓扑作详细介绍。
(1)磁力齿轮
磁力齿轮的概念最早源于20世纪初,Armstrong在专利中提出可利用磁场能进行能量传递,之后采用永磁体进行变速传动的磁力齿轮原型被提出。受限于磁体性能,磁力传动技术未能得到广泛关注。得益于80年代高性能稀土永磁的发展,磁力传动技术重新回到人们视野。日本Tsurumoto教授此后提出了几种磁力齿轮拓扑,均采用与机械齿轮原理类似的齿啮合结构,如渐开线型、涡轮蜗杆型、斜齿型等。这些结构下同一时间工作的磁极比例较少,故永磁体利用率较低。基于磁场调制原理的同心磁力齿轮最先由英国David Howe教授于2001年提出,其采用与游标电机类似的磁场调制原理[7],能够实现对永磁转子磁动势的调制,从而使两个不同极对数和转速的永磁转子的气隙磁场耦合。其同心式结构使得全部磁极同时参与传动,故永磁体利用率高,转矩密度较传统磁齿轮显著上升。另外,该结构也便于其与永磁电机进行复合,从而提升电机系统的转矩密度。因此,磁场调制型磁齿轮及其复合电机成为此后20年间磁力传动领域的主要研究方向。除了磁场调制型磁力齿轮,另外几种永磁体利用率较高的磁力齿轮结构也相继被提出,如行星磁力齿轮、少齿差偏心磁力齿轮、谐波磁力齿轮等,其中行星磁力齿轮的同心式结构同样便于实现与旋转永磁电机的径向复合。
如图2-2所示,磁场调制型磁力齿轮由少极永磁转子、磁调制环和多极永磁转子三部分组成。少极转子、多极转子以及磁调制环的极对数分别为Ph,Pl,和Ns,且满足如下关系。
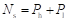
(2-1)
固定其中任一部件,另外两个旋转部件分别作为输入和输出轴,即能实现稳定的变速传动。磁力齿轮的主要优势在于:无需润滑和定期维护,其无维护寿命在十年以上;自带失步过载保护特性,能有效避免齿轮卡死风险,减少传动系统对电机的冲击;可实现无接触密封传动,在医药、石油化工、航天等领域具有不可替代的作用;可靠性高,振动噪声低,还可减少机械接触带来的摩擦损耗,提升系统效率等。相较机械齿轮,磁力齿轮的主要劣势在于减速比和转矩密度较低。
(2)游标永磁电机
游标永磁电机的形成过程如图2-3所示。在磁齿轮永磁电机中,调制单元与电枢单元均静止,因此可以去掉两者之间的间隙,将调制单元的导磁块与定子铁心直接相连。如果定子齿数与调制单元的导磁块数相同,则可以将原来的定子齿设计为开口槽结构,使定子齿槽同时实现传统齿槽和磁场调制的功能。
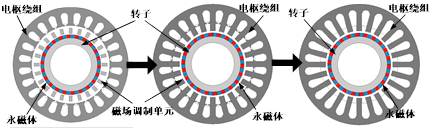
图2-3从磁齿轮永磁电机到游标永磁电机的拓扑转换过程
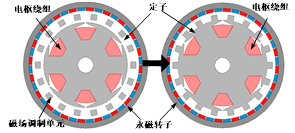
图2-4从外转子磁齿轮永磁电机到辅助齿游标永磁电机的拓扑转换过程
在游标永磁电机中,调制单元极对数Pf即为定子齿数Zs。因此为实现机电能量转换,电枢绕组极对数需要满足
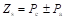
(2-2)
由于游标永磁电机中励磁单元旋转,因此其极比定义为
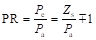
(2-3)
为了增加极比以提升转矩密度,游标永磁电机的电枢绕组极对数Pa远低于定子槽数Zs。因此,这类电机绕组跨距较大,端部较长,从而增加了电机整体体积与铜耗水平,导致其转矩密度优势的跌落。为了解决这一问题,有学者提出了具有辅助齿结构的游标永磁电机拓扑,形成过程如图2-4所示。当调制单元中导磁块的数量为定子齿数的倍数时,将导磁块附着于定子齿后,无法形成直齿结构,而是在每个定子主齿顶部连接有数个小型辅助齿,这些辅助齿起到磁场调制的作用。
根据磁场调制理论,辅助齿游标永磁电机的极槽配合满足:
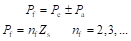
(2-4)
其极比为
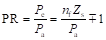
(2-5)
总体而言,游标永磁电机结构较为简单,除了定子采用开口槽,且定转子极对数不等之外,结构与传统电机完全相同,因此加工制造技术较为成熟,装配、固定也较为简单。正因为这些优点,游标永磁电机成为了近年来电机领域研究热点之一。
(3)永磁磁通反向电机
当励磁单元采用永磁体,并放置于定子侧,就得到了永磁磁通反向电机。图2-5给出了从磁场调制电机经典拓扑到磁通反向电机的演变过程。首先将励磁单元的永磁体从铁心上分离,并改变其位置,将其置于电枢与调制单元之间,且由于永磁体静止,可将其直接附着于定子表面;其次经过上述步骤后,电机内部为光滑铁心,其是否旋转对电机性能无任何影响,因此设置其与调制环同步旋转,并将导磁块附着于铁轭上,最终形成具有单气隙的拓扑。从上述演变过程可得,上述电机极槽配合选择较为灵活,只需要满足Zr=Pe±Pa的磁场调制关系即可,这种电机可称为永磁体均布型磁通反向电机。
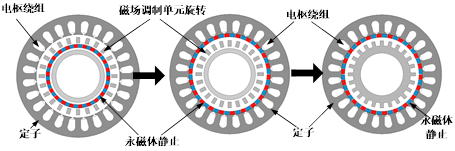
图2-5永磁体均布型磁通反向电机的演变过程
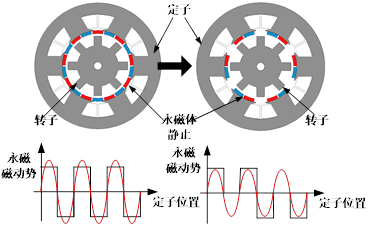
图2-6磁通反向电机拓扑的进一步演变
然而,图2-5中的电机拓扑仍不同于常见的磁通反向电机,需要在此基础上进一步演变。首先,规定永磁体极对数Pe和定子齿数Zs满足如下关系:
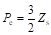
(2-6)
其次,设置定子齿宽占据整个圆周的2/3,则形成了图2-6左侧的电机拓扑;由于其中有若干磁钢放置于槽口,其对于反电势与转矩的贡献较弱,因此将其去掉,形成了图2-6右侧的拓扑,该拓扑即是文献中常见的磁通反向电机结构。
下面来分析磁通反向电机中的调制效应。需要注意的是,由于在拓扑演变的过程中,由于去掉了部分永磁体,永磁磁动势不再是正负对称的方波,而是含有含量较高的“次谐波”,其极对数为齿数的一半,如图2-6所示。或者说励磁单元极对数为Zs/2,但其中含有大量高次谐波。为了与现有磁通反向电机文献叙述一致,本节采用后一种说法。此时永磁体产生的励磁磁动势可表示为:

(2-7)
其中,Feh代表h次磁动势谐波幅值。此外,虽然永磁磁通反向电机定子槽开口较大,但此处没有永磁体,也就是励磁磁动势为零,因此槽开口比磁导的大小对于电机性能没有任何影响,即可假设定子表面光滑,只需要考虑转子开槽引入的比磁导函数:
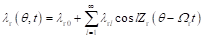
(2-8)
根据磁场调制原理,可基于式(2-7)和(2-8)求取各次空载气隙磁场分量,可分为两类,第一类为静止谐波,其极对数可表示为:
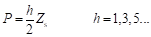
(2-9)
这类谐波不参与机电能量转换。第二类谐波为旋转谐波,其极对数可表示为:
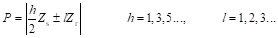
(2-10)
根据表3.2,这些谐波对应电频率只与比磁导次数l有关,l=1对应的磁密谐波均可在电枢绕组中感应基波反电势。此外,这些磁场谐波均互为齿谐波,因此,在设计电枢绕组时,只需要按照其中任意极对数绕制,即可与所有谐波交链。通常而言,定义电枢极对数为式(2-10)中l取1时最低的正整数,即
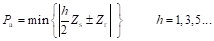
(2-11)
磁通反向电机的极比定义为
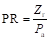
(2-12)
(4)永磁开关磁链电机
在永磁磁通反向电机中,每个定子齿被分为两部分,表面分别贴有励磁方向相反的永磁体,且相邻齿上靠近的两部分励磁方向相同。因此,可以将每个定子齿根据励磁的不同分为两部分,两者通过空隙隔开,原本具有相同励磁的部分改用轭部的单块永磁体励磁,从而得到图2-7中间的拓扑;该拓扑的励磁可进一步用放置于空隙的切向励磁永磁体代替,此时每个齿的励磁极性相比初始结构同样未发生变化,从而最终得到永磁开关磁链电机,如图3.11右图所示。
相较于磁通反向电机,永磁开关磁链电机的磁动势与磁导均发生一些变化。首先开关磁链电机的永磁体沿圆周均匀分布,若忽略转子开槽引入的磁路不对称,该电机永磁磁动势为理想方波,其极对数为Zs/2,三次谐波含量相比磁通反向电机明显降低,如图2-8所示,其数学表达式为:
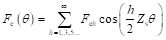
(2-13)
其中Fe1较大,而其它谐波幅值较低。开关磁链电机每个定子齿被永磁体分隔为两个小齿,而最优的永磁体宽、小齿宽与槽口宽相等。因此,定子比磁导基波极对数为2Zs,比磁导函数可表示为:
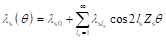
(2-14)
式中,由于定子轴线取在齿中心线的位置,而该处为永磁体,比磁导最小,因此λs1为负值。
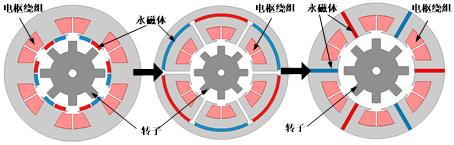
图2-7永磁磁通反向电机到开关磁链电机的拓扑演变过程
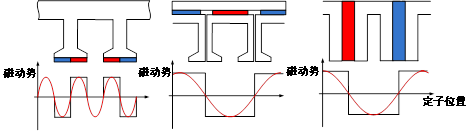
图2-8永磁开关磁链电机的磁动势
开关磁链电机的转子比磁导与磁通反向电机相同,其已经在式(2-8)中给出。但为了区分定转子比磁导,将其次数改为用lr表示。定转子均开槽下的气隙比磁导可表示为:
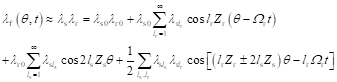
(2-15)
利用磁场调制理论可求得永磁开关磁链电机空载磁密,根据运动状态可将气隙磁场谐波分为两类,第一类为静止磁场,其不参与机电能量转换;第二类为空间旋转磁场,这些磁场电频率只和转子比磁导次数lr有关,当lr=1时,对应气隙磁场在绕组中感应基波反电势。这些谐波极对数可统一表示为:
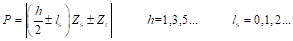
(2-16)
不难证明,满足式(2-16)的所有磁场谐波均为电枢绕组的齿谐波。因此,在设计开关磁链电机的电枢绕组时,只需将其极对数设置为满足式(2-16)的最小正整数,也就是:
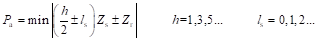
(2-17)
开关磁链电机的极比同样按照式(2-12)定义。类似于磁通反向电机,当极比增加时,开关磁链电机部分工作谐波的转矩放大系数可能反而下降,因此电机输出转矩不一定与极比正相关。此外,在某些极槽配合下,开关磁链电机采用叠绕组具备更优的转矩能力。
(5)电励磁磁场调制电机
励磁磁动势静止型磁场调制电机特点之一在于当励磁单元为直流绕组时,可将其放置于定子侧,从而避免了传统同步电机的旋转励磁问题。这类电机在航空起动/发电系统中具备优秀的潜在应用价值。电励磁磁场调制电机可分为电励磁游标磁阻电机、电励磁开关磁链电机与电励磁双凸极电机三类。
电励磁游标磁阻电机可以从永磁体均布型磁通反向电机演变得到,如图2-9所示。假设该电机励磁永磁体极对数满足
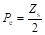
(2-18)

图2-9从磁通反向电机到电励磁游标磁阻电机的演变过程
那么每个定子齿均被单独一块永磁体励磁,且相邻齿的励磁方向相反。在这种情况下,可将每块永磁体均用励磁线圈代替,从而形成图2-9中右图所示拓扑,其即为电励磁游标磁阻电机。类似于定子永磁型电机,可求得电励磁游标磁阻电机工作磁场极对数为:
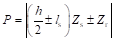
(2-19)
这类电机的极比仍可用类似式(2-11)-(2-12)的方式定义。由于其励磁部分静止,为了提升其励磁能力,可采用超导励磁绕组,相较于常规超导同步电机具备冷却方便、无电刷滑环的独特优势。
电励磁开关磁链电机拓扑如图2-10所示,其可视为直接由永磁开关磁链电机改造而来。在永磁开关磁链电机中,定子被永磁体分隔为若干个“U”型铁心,每块铁心被相邻的永磁体励磁,产生单极性励磁磁场。其中永磁体的作用可以通过横跨该“U”型铁心的励磁绕组代替。此外,为了减小励磁磁路的磁阻,可将原本分离的铁心轭部打通(该轭部在永磁电机中会增加漏磁),便得到最终的拓扑方案。由于原本放置永磁体的槽如今放置励磁绕组,因此电励磁开关磁链电机实际采用的是跨两齿绕组。
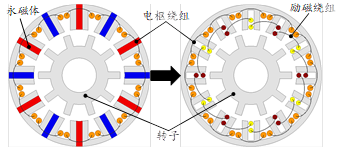
图2-10由永磁开关磁链电机到电励磁开关磁链电机的拓扑演变
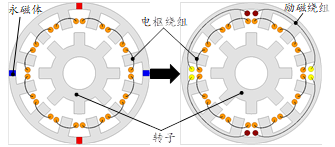
图2-11由永磁双凸极电机到电励磁双凸极电机的拓扑演变
电励磁双凸极电机拓扑如图2-11所示,其可视为直接由永磁双凸极电机改造而来。在永磁双凸极电机中,每块永磁体需要给相邻3个齿励磁,其励磁功能同样可用横跨3个齿的励磁绕组代替。然而,这种励磁方式导致的后果是1/4的槽中增设励磁导体,其槽面积需要增大。因此,在电机设计过程中,往往需要对定子齿形进行优化,从而使各个槽大小不等,便于放置励磁绕组。此外,虽然这类电机电枢为分数槽集中绕组,但绕组系数较低,且励磁绕组跨距固定为3,端部仍相对较长,这两点成为了其技术缺陷。
2.2 高性能磁场调制电机拓扑研究
(1)横向错位磁场调制型无刷双转子电机
研究并提出了一种横向错位磁场调制型无刷双转子电机(Transversely-Dislocated Magnetic-Field Modulated Brushless Double-Rotor Machine, TDMFM-BDRM),该电机是基于三维磁场调制原理工作的新型无刷双转子结构电机,它的两个转子受到实时大小相等、方向相反的电磁转矩作用,适用于对转推进系统。由于该电机两个转子上无绕组,去除了电刷和滑环机构,且TDMFM-BDRM的定子在最外侧、定子绕组无端部,既解决了传统对转永磁电机旋转绕组造成的发热严重、可靠性差、动平衡难以保证等瓶颈问题,也能避免传统无刷对转电机存在的中间定子绕组散热困难和双转子转矩实时同步控制复杂等问题。
TDMFM-BDRM的结构如图2-12所示,从外到内分别是定子、调制转子和永磁转子。TDMFM-BDRM的定子与圆筒型直线电机的定子结构类似,即定子上放置三相或多相环形绕组,且定子环形绕组沿轴向阵列排布;TDMFM-BDRM的永磁转子与传统永磁电机的永磁转子结构相同,即永磁转子永磁体沿周向阵列排布。TDMFM-BDRM的特殊之处在于中间的横向错位调制转子,如图2-13所示,它是由导磁块和非导磁支撑装置构成。
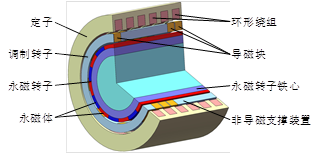
图2‑12 TDMFM-BDRM的拓扑结构
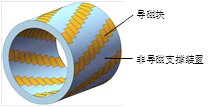
(a)调制转子的结构示意图
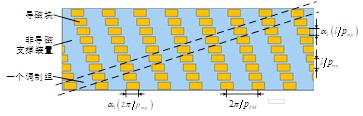
(b)调制转子的结构展开示意图
图2-13 TDMFM-BDRM调制转子的结构
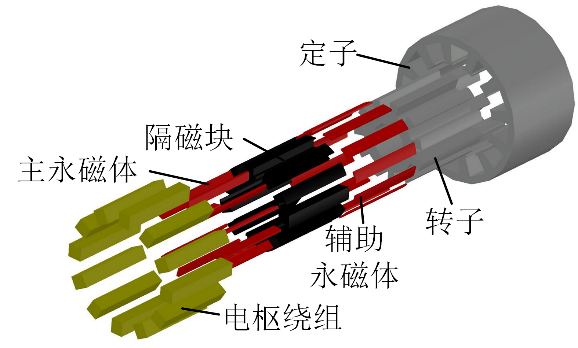
(2)交替极轮辐式游标电机结构
研究并提出了一种交替极轮辐式游标电机,如图2-14所示。研究了交替极轮辐式的磁路分布,并对转子结构中存在的主永磁体和辅助永磁体的位置、作用进行了定性分析。基于新电机模型,针对模型中涉及的的磁动式、磁导函数的解析式进行推导,基于解析模型对不同参数下的气隙磁密、反电势等与反映场调制效应相关的目标函数进行定量分析计算。
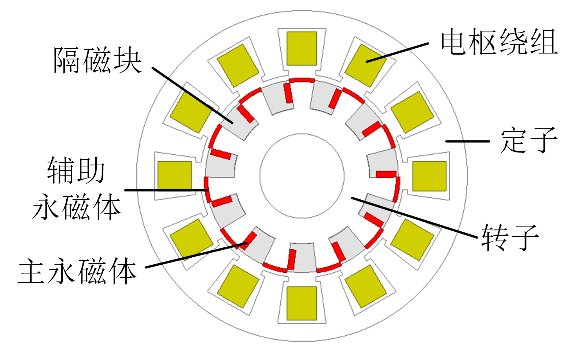
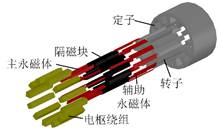
(a) 电机截面图 (b)电机3D图
图2-14交替极轮辐式游标电机结构
进一步地,本课题出一种无接触一体化永磁游标电机模型,如图2-15所示,在原有电机模型的基础上,在轴向端部加入磁齿轮,对电机进行二次自减速,用纯电磁传动结构代替机械传动结构,减小了机械损耗、无机械振动和噪声,在有限的空间内实现大减速比。一体化电机具体结构特点如下:
1)电机转子与磁齿轮内转子的外径一样大,直接进行刚性连接,且磁路互不干扰;
2)磁齿轮外转子进行了二次的减速增扭,实现了大减速比传动,其传动比为-66。
|

|
(a) 电机结构图 |
(b)磁齿轮结构图 |

|
(c)同轴转子 |
图2-15 一体化电机部件图 |
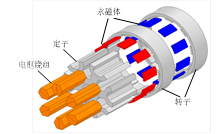
(3)外转子集中绕组交替极磁场调制电机
本课题提出了一种新型外转子交替极轴向分段磁场调制电机结构,如图2-16(a)(b)所示。该新型电机的具体结构特点如下:
1)分裂齿结构:该电机定子采用分裂齿结构,一个主齿上有两个调制极,在空间有限的情况下提升减速比且利于散热;
2)不等齿距结构:定子调制齿采用不等齿距结构,能有效消除反电势高次谐波,增加了反电势正弦度;
3)集中绕组:电枢绕组采用集中绕组的形式,减小了端部长度和相间互感,提升电机的可靠性与容错能力;
4)交替极结构:转子永磁体采用交替极结构,节省了永磁体的用量,降低电机的制造成本。

|
|
(a) |
(b) |
图2‑16 新型永磁游标电机结构(a)电机截面图. (b)电机3D图 |
2.3 建立电机稳态伺服品质与电机拓扑间的映射关系
本项目以游标永磁电机为研究对象,首次提出可实现电机转矩密度的理论上限的拓扑定向设计方法。该方法以沿气隙圆周周向分布的气隙磁导单元为研究媒介,通过定量评估各磁导微元的空载反电势贡献,基于磁导函数与气隙物理结构的映射关系,定向设计得到可以实现理论最大转矩输出的最优气隙结构。
(1)磁导微元设计
本项目所提定向设计方法的研究对象为每个气隙圆周位置上的径向气隙磁导单元,如图2-17所示。为了避免磁导微元之间的相互干扰,假设任意一个气隙圆周θsi位置的气隙磁导微元Λ(θsi)不为零,而其他位置的磁导均为零。在图2-17中,Λ0,i,Λ1,i和Λ2,i分别表示气隙磁导微元Λ(θsi)对Λ0,Λ1,Λ2的贡献大小。
实际上,磁导微元Λ(θsi)可以视为恒定磁导和所有极对数的磁导谐波的组合,因此Λ(θsi)可以被傅立叶展开为式(2-20)所示。
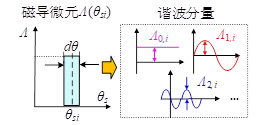
图2-17径向磁导微元及其谐波分量的示意图
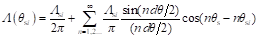
(2-20)
式中,Λsi代表磁导微元Λ(θsi)的幅值。
理论上,磁导微元的宽度dθ是无穷小的,因此式(2.95)可以进一步化简为
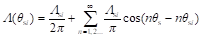
(2-21)
通过式(2-21),便可以计算得到单个磁导微元Λ(θsi)对于工作磁导谐波幅值Λj的贡献,即Λj,i。接着,可以根据机电转换原理求解出磁导微元Λ(θsi)对平均转矩Tavg的贡献,即dTavg,i,如式(2.98)所示。从该式中不难发现,Tavg=f(Λ)已经被量化为dTavg,i=f(Λsi),其中dTavg,i与Λsi成正比,比例系数Ki包含了kwv、Pmj和θmj的信息。
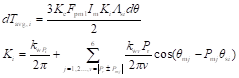
(2-22)
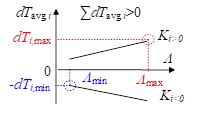
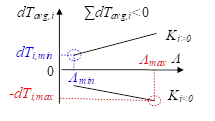
通过分析式(2-22)可知,dTavg,i在Ki>0时为正值,在Ki<0时为负值。为了使Tavg最大化,本文总结出了设计最佳磁导微元幅值Λsi的规则,以最佳分配dTavg。首先,Λsi的值是在Λmin到Λmax之间的,并且Λsi首先假定取值为Λmax。
1) 如图2-18(a)所示,如果dTavg,i之和大于0,则正dTavg,i必须取到最大值,而负dTavg,i则应该是取到最小值的。那么为了实现这个目的,当Ki>0时,Λsi等于Λmax,此时dTavg,i等于dTi,max。当Ki<0时,Λsi等于Λmin,dTavg,i等于-dTi,min。
2) 如图2-18(b)所示,如果dTavg,i之和小于0,则正dTavg,i必须取到最小值,而负dTavg,i应该是取到最大值的。那么为了实现这个目的,当Ki>0时,Λsi等于Λmin,dTavg,i等于dTi,min。当Ki<0时,Λsi等于Λmax且dTavg,i等于-dTi,max。
从上述的规则中可以发现Λsi的最佳取值只可能是Λmax或者Λmin。
|
|
(a)dTavg,i之和大于0 |
(b)dTavg,i之和小于0 |
图2-18Λsi最优值的设计规则 |
(2)气隙拓扑设计
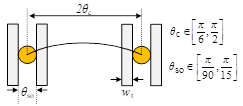
列出所有可行的集中绕组结构Nwi(θs),并计算出所有的fmax(Λ)后,可以得到fmax(Λ)的全局最大值。对于集中绕组结构的函数Nwi(θs),影响其取值的是集中绕组的两个结构参数槽开口宽度θso和线圈跨距θc,如图2-19所示。还应注意的是,每个线圈两旁应当有两个齿,齿的宽度为wt(本项目设计wt至少为3deg),满足
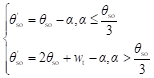
(2-23)
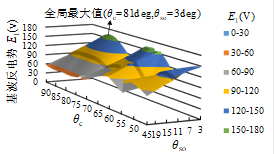
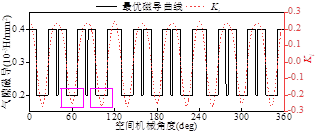
当忽略铁磁材料中的饱和时,E1与Tavg之间存在直接的对应关系。为了便于通过有限元计算软件(FEA)对解析结果进行验证,后文将以空载反电势基波幅值E1代替平均转矩Tavg进行计算。图2-20中给出了E1,max关于(θc,θso)的曲面图,其中E1,max的全局最大值为163.6V,图2-21中给出了最大E1相应的Ki和磁导分布曲线,其中,正Ki之和大于负Ki之和,这意味着dTavg,i之和大于0。根据上文中所总结的Λsi最优值设计规则可知,突出显示区域的dTavg,i为负值。为了尽可能减少负的dTavg,突出显示区域中,尤其是中央部分的Λsi应尽可能小。最后,通过气隙拓扑量化构造方法所设计的表贴式游标永磁电机拓扑如图2-22所示。
|
|
图2-19 绕组的结构参数示意图 |
图2-20 E1,max关于(θc,θso)的曲面图 |
|
|
图2-21 最优磁导曲线示意图 |
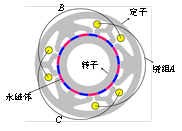
图2-22磁导定向构造方法设计的表贴式游标永磁电机拓扑 |

|
|
(a)反电势波形 |
(b)谐波频谱 |
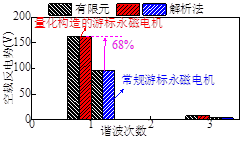
图2-23两种游标永磁电机的空载反电势比较 |
定向设计游标永磁电机与常规游标电机的空载反电势的波形和谐波频谱如图2-23所示。解析计算的结果与有限元结果有较好的吻合。谐波分析显示,两台电机的基波反电势幅值E1分别为162V和96.4V,所提出的游标永磁电机的E1比常规游标永磁电机的E1高68%。这说明,前者的转矩输出能力提升了68%。
三、研究成果
本项目出版专著2部,发表(含录用)论文36篇(其中SC接收/发表期刊论文24篇、EI会议论文4篇、中文核心期刊论文8篇),已授权中国发明专利16件、美国发明专利2件,公开中国发明专利4件。获2024年IEEE工业应用学会杰出成就奖、湖北省技术发明一等奖等学术奖励13项;培养博士研究生15名、硕士研究生7名,获国家自然科学基金优秀青年基金1人,获中国电工技术学会科学技术奖青年科技奖1人,获博士后创新人才支持计划1人。